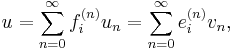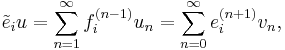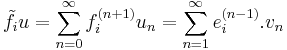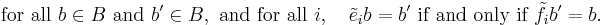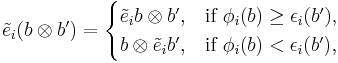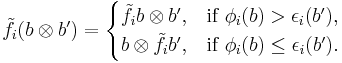Crystal base
In algebra, a crystal base or canonical base is a base of a representation, such that generators of a quantum group or semisimple Lie algebra have a particularly simple action on it. Crystal bases were introduced by Kashiwara (1990) and Lusztig (1990) (under the name of canonical bases).
Contents |
Definition
As a consequence of the defining relations for the quantum group 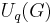 ,
, 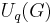 can be regarded as a Hopf algebra over
can be regarded as a Hopf algebra over 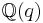 , the field of all rational functions of an indeterminate q over
, the field of all rational functions of an indeterminate q over 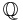 .
.
For simple root 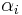 and non-negative integer
and non-negative integer  , define
, define ![e_i^{(n)} = e_i^n/[n]_{q_i}!](/2012-wikipedia_en_all_nopic_01_2012/I/8976ce919a5242c2b7f68f1b3fdeab24.png) and
and ![f_i^{(n)} = f_i^n/[n]_{q_i}!](/2012-wikipedia_en_all_nopic_01_2012/I/5aadd7fa034c7b3a8df494e4a41ec8e8.png) (specifically,
(specifically, 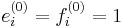 ). In an integrable module
). In an integrable module  , and for weight
, and for weight  , a vector
, a vector 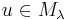 (i.e. a vector
(i.e. a vector  in
in  with weight
with weight  ) can be uniquely decomposed into the sums
) can be uniquely decomposed into the sums
where 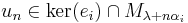 ,
, 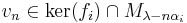 ,
, 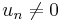 only if
only if 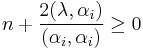 , and
, and 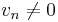 only if
only if 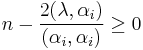 . Linear mappings
. Linear mappings 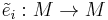 and
and 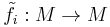 can be defined on
can be defined on 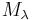 by
by
Let  be the integral domain of all rational functions in
be the integral domain of all rational functions in 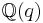 which are regular at
which are regular at 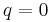 (i.e. a rational function
(i.e. a rational function 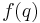 is an element of
is an element of  if and only if there exist polynomials
if and only if there exist polynomials 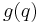 and
and 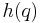 in the polynomial ring
in the polynomial ring ![{\Bbb Q}[q]](/2012-wikipedia_en_all_nopic_01_2012/I/5f7133b0b8d1ff59e3fd76be82c47762.png) such that
such that 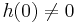 , and
, and 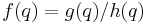 ). A crystal base for
). A crystal base for  is an ordered pair
is an ordered pair 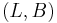 , such that
, such that
-
 is a free
is a free  -submodule of
-submodule of  such that
such that 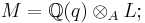
-
 is a
is a 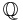 -basis of the vector space
-basis of the vector space 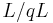 over
over 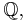
-
 and
and  , where
, where 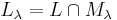 and
and 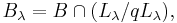
-
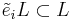 and
and 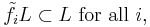
-
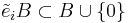 and
and 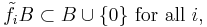
To put this into a more informal setting, the actions of 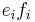 and
and 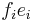 are generally singular at
are generally singular at 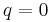 on an integrable module
on an integrable module  . The linear mappings
. The linear mappings 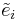 and
and 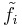 on the module are introduced so that the actions of
on the module are introduced so that the actions of 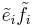 and
and 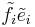 are regular at
are regular at 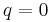 on the module. There exists a
on the module. There exists a 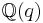 -basis of weight vectors
-basis of weight vectors 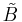 for
for  , with respect to which the actions of
, with respect to which the actions of 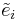 and
and 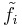 are regular at
are regular at 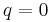 for all i. The module is then restricted to the free
for all i. The module is then restricted to the free  -module generated by the basis, and the basis vectors, the
-module generated by the basis, and the basis vectors, the  -submodule and the actions of
-submodule and the actions of 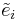 and
and 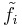 are evaluated at
are evaluated at 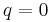 . Furthermore, the basis can be chosen such that at
. Furthermore, the basis can be chosen such that at 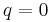 , for all
, for all  ,
, 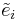 and
and 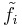 are represented by mutual transposes, and map basis vectors to basis vectors or 0.
are represented by mutual transposes, and map basis vectors to basis vectors or 0.
A crystal base can be represented by a directed graph with labelled edges. Each vertex of the graph represents an element of the 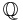 -basis
-basis  of
of 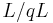 , and a directed edge, labelled by i, and directed from vertex
, and a directed edge, labelled by i, and directed from vertex 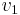 to vertex
to vertex 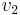 , represents that
, represents that 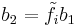 (and, equivalently, that
(and, equivalently, that 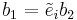 ), where
), where 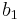 is the basis element represented by
is the basis element represented by 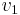 , and
, and 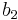 is the basis element represented by
is the basis element represented by 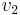 . The graph completely determines the actions of
. The graph completely determines the actions of 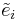 and
and 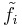 at
at 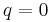 . If an integrable module has a crystal base, then the module is irreducible if and only if the graph representing the crystal base is connected (a graph is called "connected" if the set of vertices cannot be partitioned into the union of nontrivial disjoint subsets
. If an integrable module has a crystal base, then the module is irreducible if and only if the graph representing the crystal base is connected (a graph is called "connected" if the set of vertices cannot be partitioned into the union of nontrivial disjoint subsets 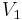 and
and 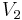 such that there are no edges joining any vertex in
such that there are no edges joining any vertex in 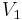 to any vertex in
to any vertex in 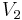 ).
).
For any integrable module with a crystal base, the weight spectrum for the crystal base is the same as the weight spectrum for the module, and therefore the weight spectrum for the crystal base is the same as the weight spectrum for the corresponding module of the appropriate Kac–Moody algebra. The multiplicities of the weights in the crystal base are also the same as their multiplicities in the corresponding module of the appropriate Kac–Moody algebra.
It is a theorem of Kashiwara that every integrable highest weight module has a crystal base. Similarly, every integrable lowest weight module has a crystal base.
Tensor products of crystal bases
Let  be an integrable module with crystal base
be an integrable module with crystal base 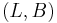 and
and 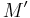 be an integrable module with crystal base
be an integrable module with crystal base 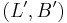 . For crystal bases, the coproduct
. For crystal bases, the coproduct  , given by
, given by 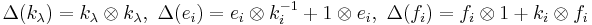 , is adopted. The integrable module
, is adopted. The integrable module 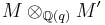 has crystal base
has crystal base 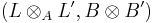 , where
, where 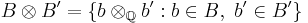 . For a basis vector
. For a basis vector 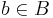 , define
, define 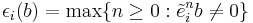 and
and 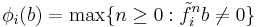 . The actions of
. The actions of 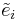 and
and 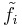 on
on 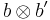 are given by
are given by
The decomposition of the product two integrable highest weight modules into irreducible submodules is determined by the decomposition of the graph of the crystal base into its connected components (i.e. the highest weights of the submodules are determined, and the multiplicity of each highest weight is determined).
References
- Jantzen, Jens Carsten (1996), Lectures on quantum groups, Graduate Studies in Mathematics, 6, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0478-0, MR1359532, http://books.google.com/books?id=uOGqPjjVt0AC
- Kashiwara, Masaki (1990), "Crystalizing the q-analogue of universal enveloping algebras", Communications in Mathematical Physics 133 (2): 249–260, ISSN 0010-3616, MR1090425, http://projecteuclid.org/getRecord?id=euclid.cmp/1104201397
- Lusztig, G. (1990), "Canonical bases arising from quantized enveloping algebras", Journal of the American Mathematical Society 3 (2): 447–498, doi:10.2307/1990961, ISSN 0894-0347, MR1035415
External links
- Crystal basis in ncatlab